[最も選択された] y=x^2 2x-8 in vertex form 289826

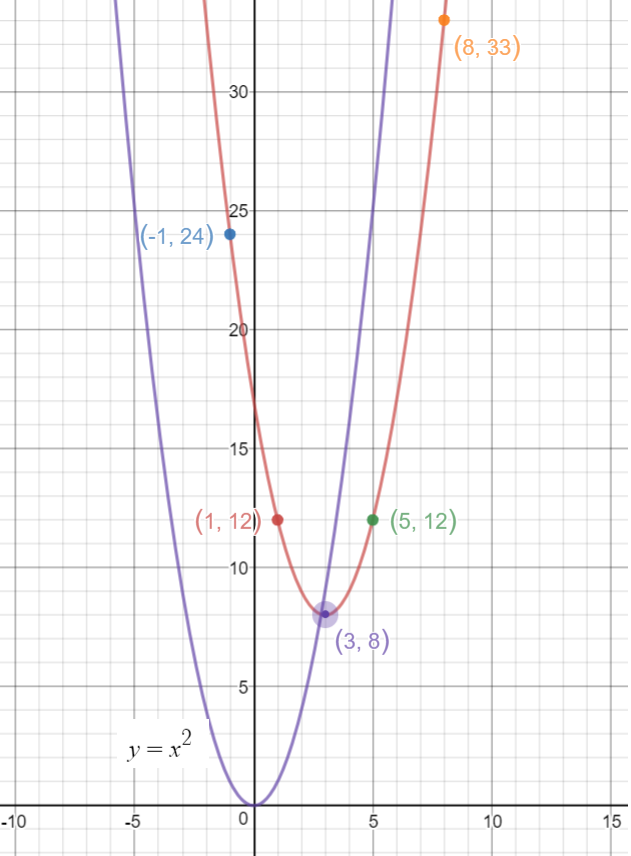
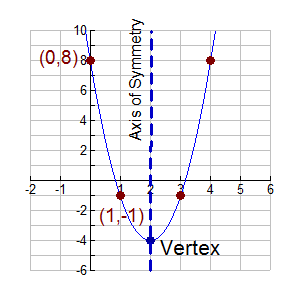
Suppose a parabola has a vertex (4,7) and also passes through the point (3,8) Write the equation of the parabola in vertex form f(x)=a(xh)^2k I believe h=4 k=7 Not sure what to do from here MathFrom this chart, we see that the parabola y = x 2 contains the points (3, 9) and (4, 16) On the other hand, he parabola y = 2x 2 contains the points (3, 18) and (4, 32) On the first equation, y =

Y=x^2 2x-8 in vertex form- heart 170 profile kim10g Answer The correct answer is y = 8 (x 2)^2 15 Stepbystep explanation I just got the question correctTiger shows you, step by step, how to solve YOUR Quadratic Equations 4(x1)^2=36^ by Completing the Square, Quadratic formula or, whenever possible, by FactoringFree factor calculator Factor quadratic equations stepbystepA) y = 2x 2 12x 16 B) y = 2x (x 6) 16 C) y = 2 (x 3) 2 (2) D) y = (x 2) (2x 8) Answer If you know the vertex form of an equation y = a (x h) 2 k then you will notice that

Y=x^2 2x-8 in vertex formのギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Y=x^2 2x-8 in vertex form」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Y=x^2 2x-8 in vertex form」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Y=x^2 2x-8 in vertex form」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Y=x^2 2x-8 in vertex form」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Y=x^2 2x-8 in vertex form」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Y=x^2 2x-8 in vertex form」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Y=x^2 2x-8 in vertex form」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

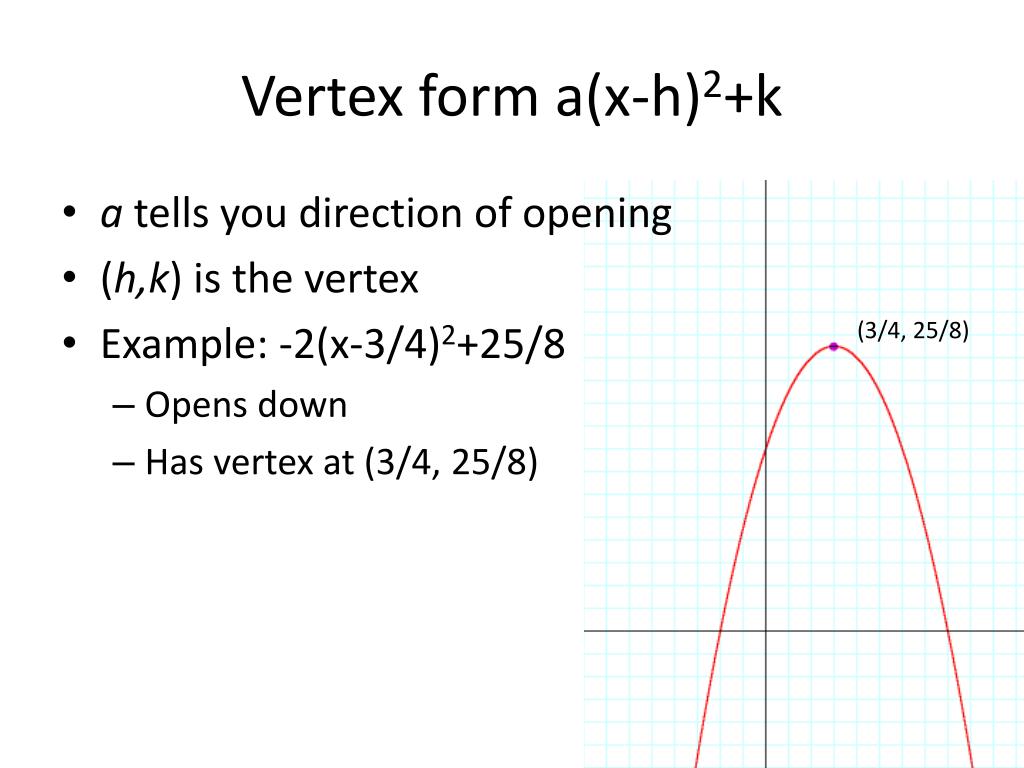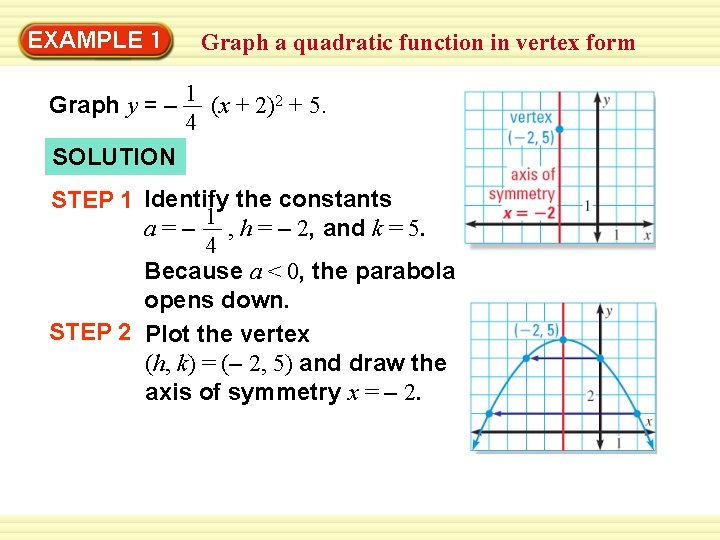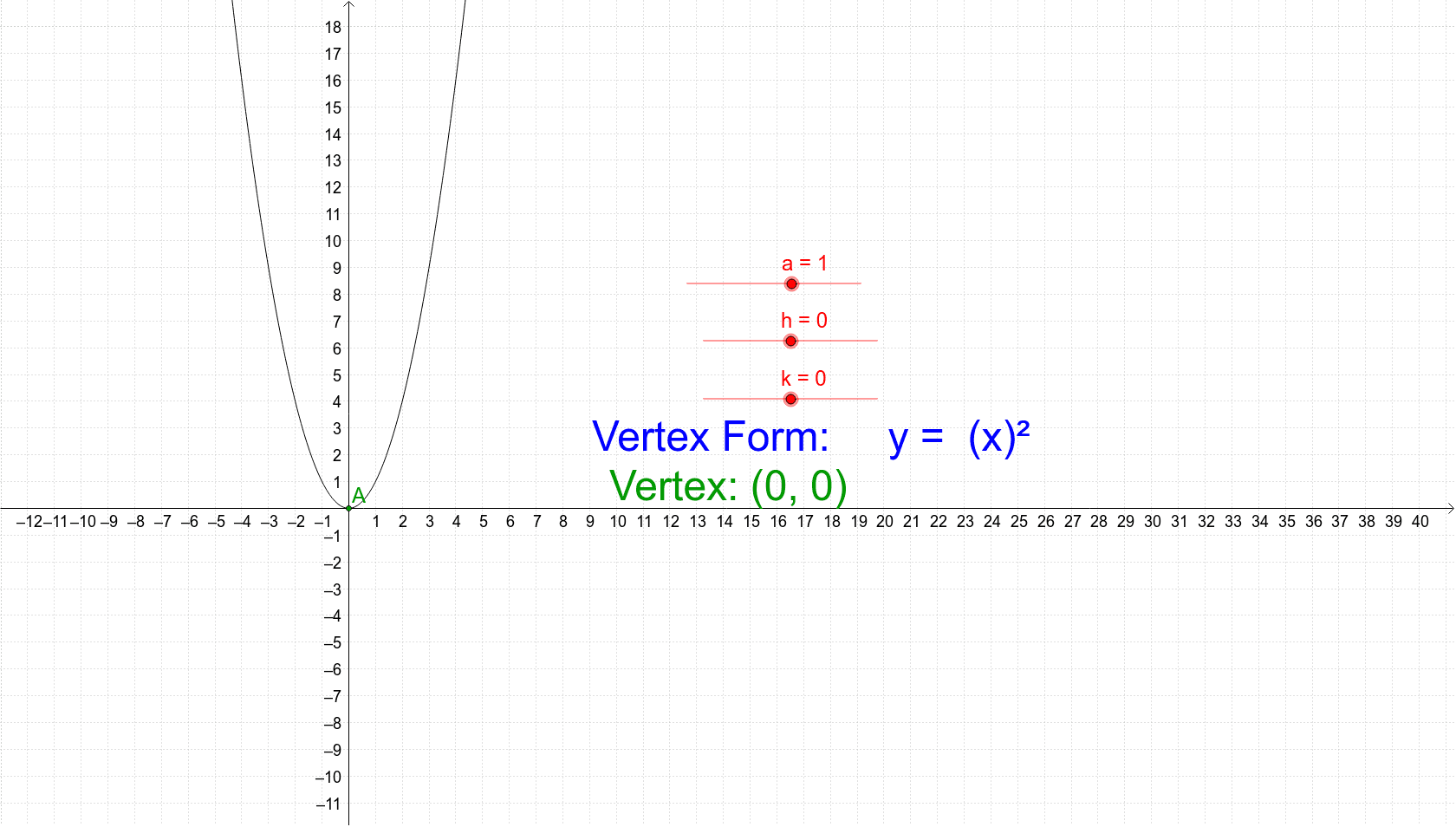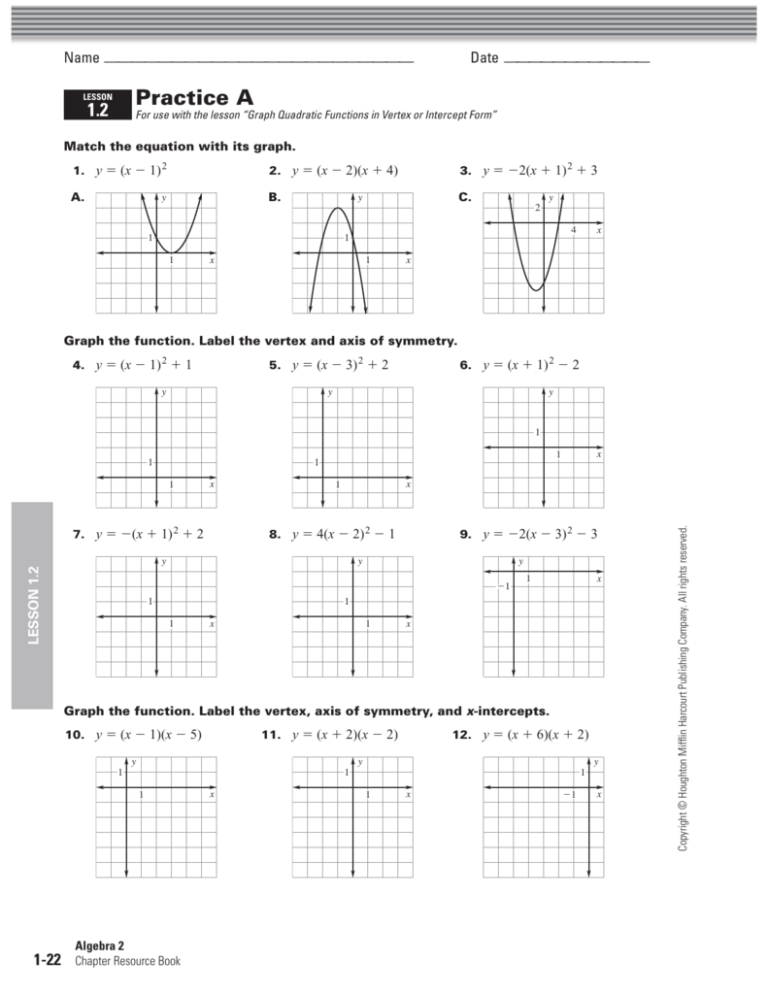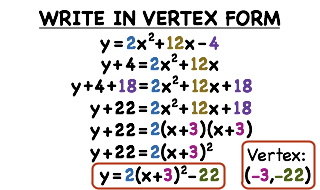「Y=x^2 2x-8 in vertex form」の画像ギャラリー、詳細は各画像をクリックしてください。

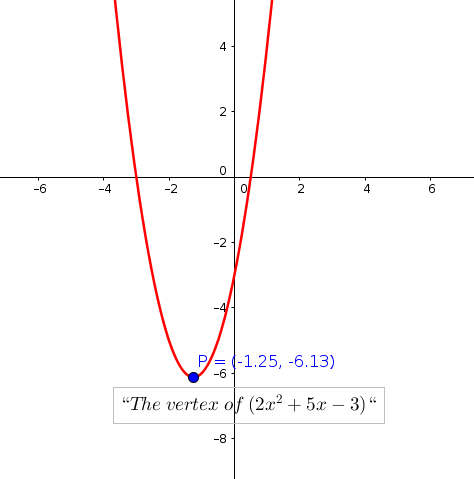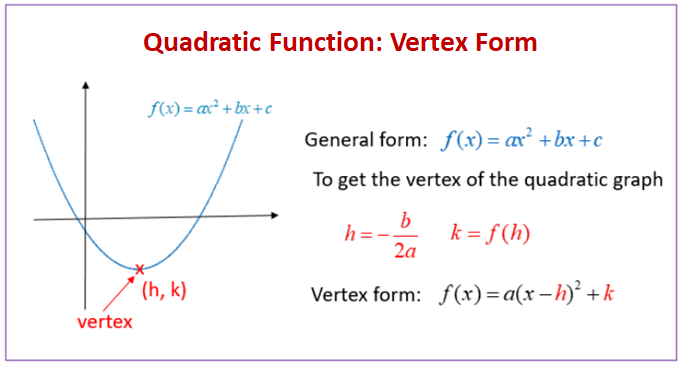
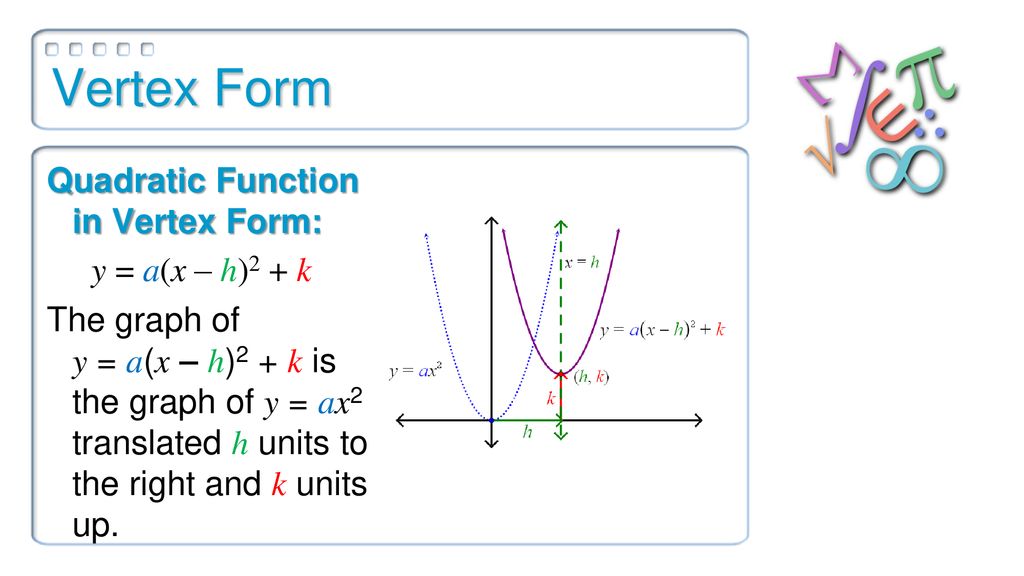
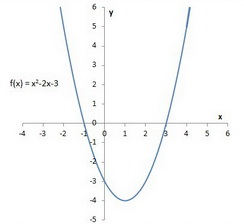
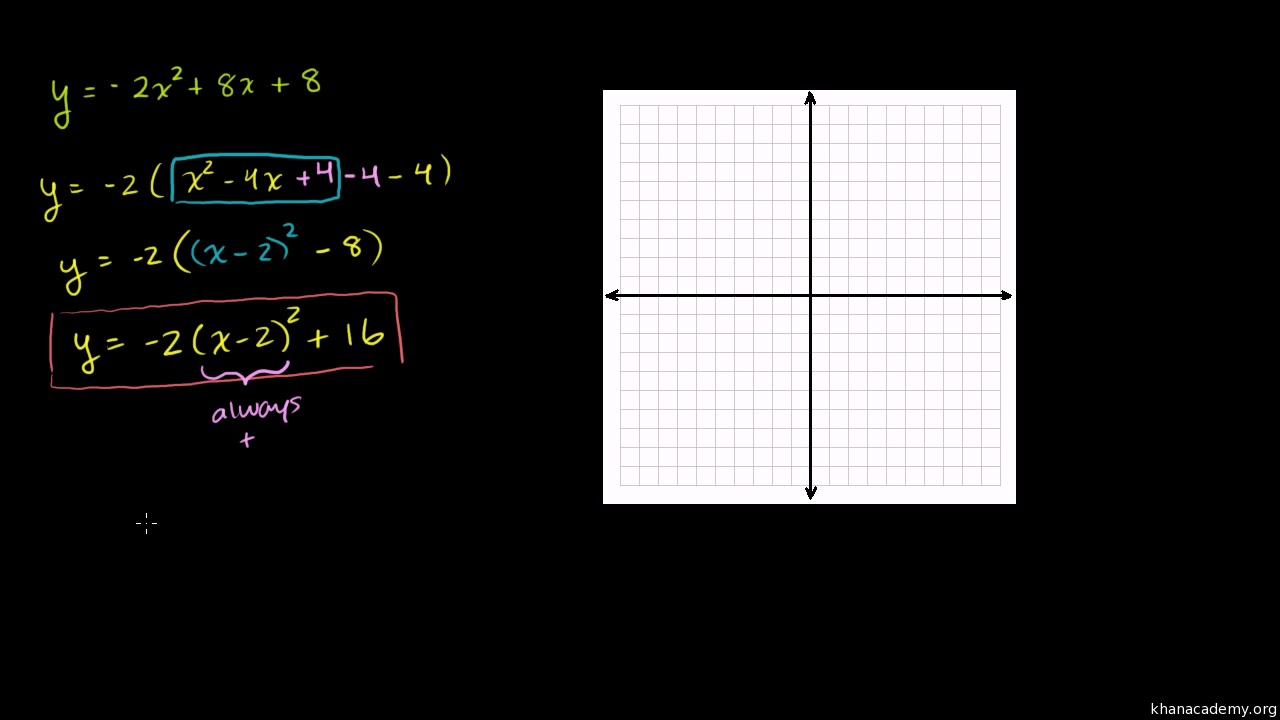
Subtract y from both sides x^ {2}2xy8=0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x=\frac {2±\sqrt {2^ {2}4\left (y8\right)}} {2}最も選択された y=x^2 2x8 in vertex form Y=x^22x8 in vertex form The vertex form is a special form of a quadratic function From the vertex form, it is easily visible where the maximum or minimum point (the vertex) of the parabola is The number in brackets gives (trouble spot up to the sign!) the xcoordinate of the vertex, the number at the end of the form gives the